When your supply chain is small — with just one factory, one product, one DC and a single group of customers — decision-making is straightforward and quick. However, as supply chains grow more complex, involving thousands of suppliers, materials,various transportation models, multiple factories and DCs and customer locations across different regions and countries, decision-making becomes hugely complex.
And often such growth of complexity has been rarely well designed; instead, it is often inherited from a series of historical coincidences, such as acquisitions and mergers, opportunistic expansion, and tactical restructuring.
This unpredictable evolution leaves huge room for optimization.
Determining where to source your product, where to place distribution centers (DCs), how much inventory should you keep, optimizing shipping routes from suppliers to factories, and then to DCs and customers requires balancing thousands of variables.
If lucky, experienced decision makers could improve supply efficiencies but they can never be sure if there were better ideas that haven’t been explored.
Without mathematical optimization, decisions would rely on intuition rather than data-driven insights.
Mathematical optimization tackles this challenge by using advanced algorithms to analyze vast amounts of data and calculate the most optimal decisions. It not only ensures that costs are minimized and customer services are maintained or improved but also enhances overall supply chain resilience and sustainability.
Keep reading to discover how mathematical optimization transforms your supply chain, making it more cost efficient and resilient in the face of complexity and uncertainty.
Mathematical Approaches to Supply Chain Network Design
The main aim of supply chain network design is to achieve optimal balance between end to end supply chain cost, service levels. It also manages production, procurement, inventory, facility, transportation costs, and associated risks effectively.
Decision variables in network design optimization models typically include:
- Number and locations of facilities (plants, DCs, warehouses)
- Production quantities at each manufacturing facility and production line
- Inventory levels at each stocking location
- Transportation modes and routes between facilities
- Customer allocation to stocking locations
- The optimal plan for consolidating orders into shipments
Mathematical optimization techniques, such as mixed-integer programming and stochastic programming, are employed to identify the network configuration. It minimizes total costs (including facility, production, inventory, and transportation costs) while satisfying demand and other operational constraints.
Optimization enables companies to evaluate numerous “what-if” scenarios and make informed strategic decisions about their supply chain network structure.
It helps balance tradeoffs between factors like transportation costs, inventory costs, customer service levels, and risk mitigation. With an optimized network design, companies can achieve significant cost savings, improve operational efficiency, and enhance customer service.
Why is Mathematical Optimization Important?
Mathematical optimization is crucial for supply chain management. It enables companies to make better, more informed decisions that can significantly improve operational efficiency, reduce costs, and increase profitability.
In today’s complex global supply chains, there are countless variables and constraints to consider, making it nearly impossible for humans to manually evaluate all possible scenarios and identify the optimal solution.
By leveraging advanced mathematical algorithms and powerful computing capabilities, optimization techniques can rapidly analyze vast amounts of data, taking into account various factors such as demand patterns, production capacities, transportation networks, inventory levels, and resource constraints.
Compared to manual decision-making processes, which often rely on intuition, experience, and simplified assumptions, mathematical optimization provides the following key benefits:
- Improved Decision Quality: Optimization models can evaluate a large number of scenarios and constraints simultaneously. They identify solutions that may not be apparent to human decision-makers. This leads to better-informed decisions that maximize efficiency and profitability.
- Cost Savings: By optimizing resource allocation, inventory levels, transportation routes, and other supply chain elements, companies can significantly reduce operational costs, such as transportation expenses, inventory carrying costs, and production costs.
- Increased Agility: Optimization models can quickly adapt to changing conditions, such as fluctuations in demand, supply disruptions, or shifts in market conditions. This agility enables companies to rapidly adjust their supply chain strategies and minimize the impact of disruptions.
- Improved Customer Service: By optimizing inventory levels, production schedules, and delivery routes, companies can improve their ability to meet customer demand in a timely and cost-effective manner, enhancing customer satisfaction and loyalty.
- Risk Mitigation: Optimization techniques can be used to analyze various risk scenarios and identify strategies to mitigate potential disruptions, such as supply shortages, transportation delays, or natural disasters.
- Competitive Advantage: By leveraging mathematical optimization to streamline operations and reduce costs, companies can gain a competitive edge in the market, enabling them to offer more competitive pricing or invest in other areas of growth.
- Corporate ESG: By leveraging mathematical optimization you can optimize the corporate carbon emissions level and help to achieve the ESG goal.
Problems of Building Optimization Models In-House
Developing custom mathematical optimization models from scratch is an extremely challenging and resource-intensive endeavor. It requires a highly specialized team with expertise spanning multiple domains, including programming, mathematical modeling, operations research, and deep industry knowledge of the specific supply chain problem being addressed.
Precision in Mathematical Formulation
One of the primary difficulties lies in translating the intricate business problem into a precise mathematical formulation. This involves identifying and quantifying all relevant decision variables, constraints, and objectives, which can be an intricate and error-prone process, especially for complex supply chain networks with numerous interdependencies.
Challenge in Algorithm Development
Once the mathematical model is formulated, the next hurdle is developing robust algorithms and solution techniques to solve the optimization problem efficiently. This often requires advanced knowledge of operations research techniques, such as linear programming, mixed-integer programming, or heuristic approaches, depending on the nature and complexity of the problem.
Furthermore, implementing these algorithms and integrating them with a suitable mathematical solver or optimization engine can be a significant programming challenge, requiring expertise in areas like parallel computing, data structures, and algorithm design.
Validation and Testing Issues
Another critical aspect is ensuring the accuracy and validity of the optimization model and its solutions. This typically involves extensive testing, validation, and calibration against real-world data and scenarios, which can be time-consuming and require close collaboration with subject matter experts and stakeholders.
Maintaining and updating custom optimization models can also be a significant burden, as changes in business requirements, constraints, or objectives may necessitate extensive modifications to the underlying mathematical formulations and algorithms.
Financial Burden
In addition to the technical challenges, developing custom optimization models from scratch often requires substantial financial and human resources. Assembling a team with the necessary expertise in mathematical modeling, operations research, programming, and domain knowledge can be costly and may not be feasible for many organizations.
Overall, while building optimization models in-house can provide tailored solutions for specific supply chain problems, it is a complex and resource-intensive endeavor that requires significant expertise, time, and financial investment.
For many organizations, leveraging pre-built optimization platforms or solutions can be a more efficient and cost-effective approach, especially when the required functionality and flexibility are available.
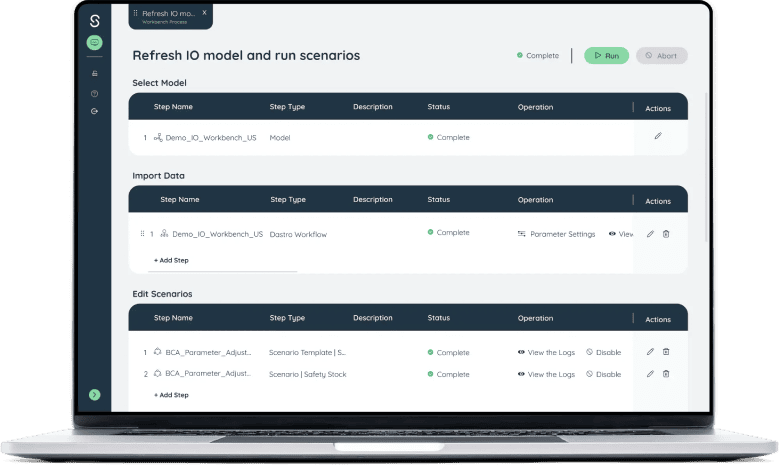
Using Pre-Built Optimization Platforms Like Sophus X
Rather than building optimization models from scratch in-house, which is a complex and resource-intensive endeavor, companies can leverage pre-built supply chain optimization platforms like Sophus X.
These platforms offer several advantages over custom development:
- Speed and Agility: Quickly deploy and configure for immediate optimization.
- Cost-Effective: Avoid high upfront and ongoing development costs.
- Expertise and Best Practices: Benefit from industry-specific algorithms and proven methods.
- Scalability and Flexibility: Adapt easily to changing business needs and scale operations.
- Ease of Use: User-friendly interfaces simplify complex tasks for non-technical users.
- Continuous Innovation: Access cutting-edge optimization techniques through ongoing platform enhancements.
Sophus X Platform Overview
Sophus X is a supply chain optimization platform that provides pre-built modeling capabilities and optimization algorithms to solve complex supply chain problems. It enables businesses to quickly implement mathematical optimization without the need for extensive in-house development efforts.
The platform offers a range of optimization modules tailored to different supply chain functions, including:
- Supply Chain Network Design
- Capacity Planning
- Inventory Optimization
- Production Modeling and Optimization
- Sales and Operations Planning (S&OP)
- Replenishment Optimization
Sophus X’s optimization engine leverages advanced mathematical algorithms and solvers to analyze vast amounts of data and identify optimal solutions.
The platform is designed to handle complex constraints, multiple objectives, and large-scale decision variables, making it suitable for intricate supply chain networks.
Sophus X Case Studies: Mathematical Optimization in Action
Sophus utilizes the fastest and most scalable mathematical algorithms to ensure quick and accurate optimization and simulation. This accelerates your network design and planning processes, improves decision-making efficiency, and allows for the construction of much larger models, thus enabling more use cases.
Here’s how Sophus has made significant impacts with these businesses:
Lee Kum Kee’s Growth
Lee Kum Kee faced challenges with high transportation costs, inventory management, and fluctuating demand. They adopted Sophus, an advanced supply chain platform utilizing mathematical optimization.
Sophus optimized transportation routes, minimized costs, and reduced delivery times. It also enabled accurate demand forecasting for efficient inventory management and scenario planning to simulate operational changes.
By leveraging mathematical optimization through Sophus, Lee Kum Kee achieved over $20 million in cost savings, streamlined operations, reduced waste, and enhanced customer satisfaction through informed, data-driven decisions.
Optimizing Inventory in Pharmaceuticals
In the pharmaceutical industry, another client transformed efficiency through Sophus’ advanced mathematical optimization capabilities. Faced with challenges such as fluctuating demand and stringent regulatory standards, they adopted Sophus to systematically optimize inventory management.
Sophus analyzed 25 critical factors affecting inventory levels in real-time and implemented adjustments accordingly.
The result? A significant 6% cost savings in inventory management. Sophus integrates advanced AI and data automation, empowering organizations to make informed decisions, reduce costs, and enhance service levels effectively.
Simplifying Mathematical Optimization with Sophus X
Mathematical optimization effectively manages the complexity of countless variables in supply chain decisions. Many people feel overwhelmed when trying to make these decisions on their own, often relying on intuition rather than data. This can lead to inefficiencies and increased costs.
However, platforms like Sophus X can save you from this hassle. Sophus X uses advanced mathematical optimization techniques to streamline your supply chain, ensuring optimal decisions at every step.
By integrating Sophus X into your operations, you can enhance efficiency, reduce costs, and gain a competitive edge.
Don’t get stuck in the complexities—opt for Sophus X and transform your supply chain management today.
FAQs
What are the mathematical models used in the optimization of supply chains?
Mathematical models used in supply chain optimization include linear programming, integer programming, mixed-integer programming, network models, and simulation models. These models help in decision-making processes like inventory management, transportation, and production planning.
How is mathematics used in supply chains?
Mathematics is used in supply chains to improve efficiency and reduce costs. It helps in forecasting demand, managing inventory, optimizing routes for transportation, scheduling production, and analyzing data to make informed decisions.
What is mathematical optimization?
Mathematical optimization involves finding the best solution from a set of possible choices, given certain constraints. It uses mathematical techniques to maximize or minimize a function, such as cost or profit, under specified conditions.
What is optimization in supply chain management?
Optimization in supply chain management is the process of making the supply chain as efficient and cost-effective as possible. This involves optimizing various aspects like inventory levels, production schedules, transportation routes, and demand forecasting to improve overall performance.
What are mathematical models and optimization?
Mathematical models are representations of real-world systems using mathematical equations and expressions. Optimization involves using these models to find the best possible solutions to problems within given constraints, often with the goal of maximizing or minimizing some objective function.
